7で割り切れるかはグラフでわかる

Divisibility by 7 is a Walk on a Graph, by David Wilson
が面白かったので拙訳を。

--

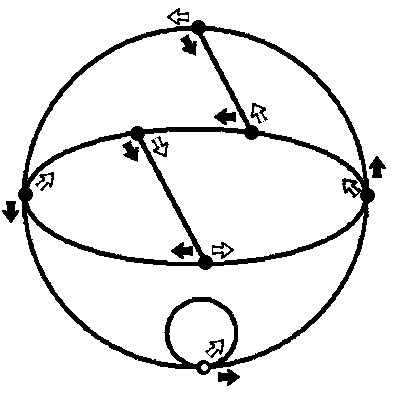
整数nを決める。
グラフの一番下の小さな白い点から スタートして、nの各桁の数字dについて、 d個の黒い矢印をたどっていく。
そして次の桁の数字に行くときに、 白い矢印を1つ分進む。

例えばn=325なら、黒い矢印を3個、 白い矢印を1個、黒い矢印を2個、 白い矢印を1個、黒い矢印を5個、の順にたどる。

白い点に戻ってきていればnは7で割り切れる。
(訳注: 白い点から黒い矢印をいくつ進んだかが 7で割った余りに対応する)

特段びっくりするようなことじゃないけど、 グラフが平面で表せるっていうのはいいね。
--

What is the process of creating this automata for checking divisibility by 7?
に解説が出ているが、黒矢印は単純に1を足すことに対応していて、 白矢印は10倍した数字を7で割った余りに移動することに対応している。
つまり、 ０→0 ↓ １→3 (10=7×1+3) ↓ ２→6 (20=7×2+6) ↓ ３→2 (30=7×4+2) ↓ ４→5 (40=7×5+5) ↓ ５→1 (50=7×7+1) ↓ ６→4 (60=7×8+4) ↓ 0→0 ・・・ で、下に進むのが黒矢印、右に進むのが白矢印となっている。
これも当然だけど、7×xのxを白矢印の順にたどると142857になる。